Scene Breakdown: Sky Aquarium

About

A while ago, I created a Dynamic Water Demo in the Godot Engine. It showed how to write a realistic water wave simulation entirely within Godot using fragment shaders.

Just recently Nintendo brought a timeless classic, Super Mario Galaxy, to the Switch. I could obvisously not resist the urge to play through it for a fourth time and got back into the game. Not far in, I stumbled upon planets such as this:

Image from mariowiki.com

While these do not exhibit any elaborate water physics, they still inspired me. I wanted to see whether applying the same principles I had already used successfully before would work on a sphere as well as it did on a flat plane. I thus started working on a small scene that would showcase whether something like this was possible using solely built-in Godot functionality (plus some preprocessing in Blender).

I like to think that I succeeded in this mission and in this post I will do what I will call a “scene breakdown”: walk through the process of creating the most important parts of the scene.

Recap: Dynamic Water on a Plane

In my Dynamic Water Demo I used the finite difference method to solve the wave equation. For this, the flat water surface as divided into a rectangular grid. After that, for each time step, the grid points were updated by taking the values of their neighbours (in the previous two time steps) into account.

Five-point stencil for solving the wave equation in 2 dimensions on a flat surface.

When applying the water simulation to a sphere, many principles will remain the same or very similar and I will not explain them in detail here. Give the original demo a read if you are hungry for more details.

Discretising a Sphere

If we want to map our simulation to a sphere, we need to choose a different discretisation. We can use meshes for this as they are just discrete representation of 3D shapes. The meshes vertices are then the grid points which are connected by edges. Probably the two most commong ways of meshing (or discretising) spheres are UV spheres and icospheres. If you have ever opened Blender or any other 3D modelling software before, you will probably be familier with them:

Constructing UV or icospheres in blender.

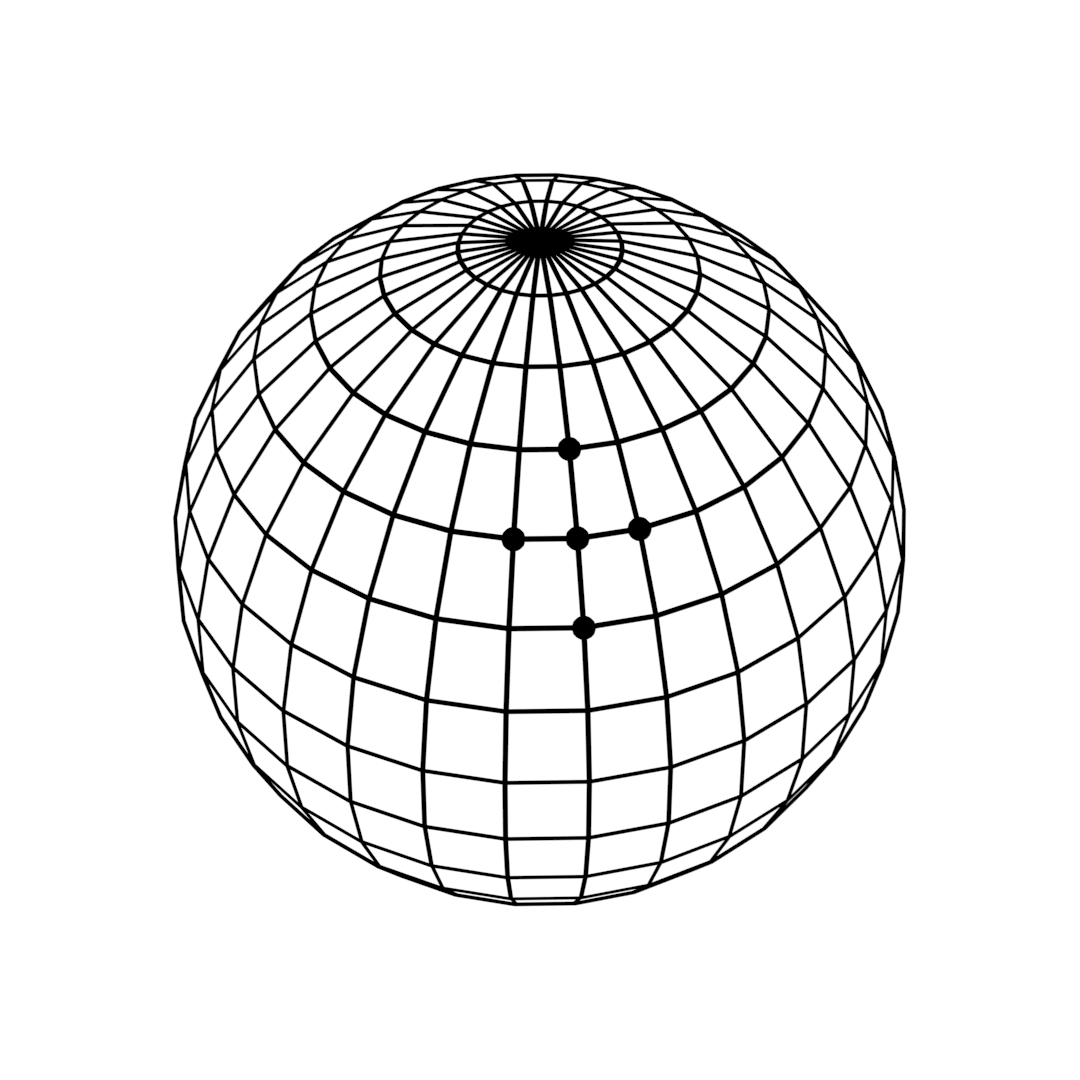
UV spheres use the same principle as mapping the earth’s surface using lattitude and longitude. You may notice that the UV sphere actually has similar properties to the rectangular grid from above. (Almost) every vertex has four neighbours. But as with earth, all “meridians” converge at the “poles” of the sphere. As a side effect, the distance between points varies depending on how close to the poles one is. For a smooth simulation, however, a more uniform discretisation where each and every vertex has approximately the same distance to its neighbours is desirable.

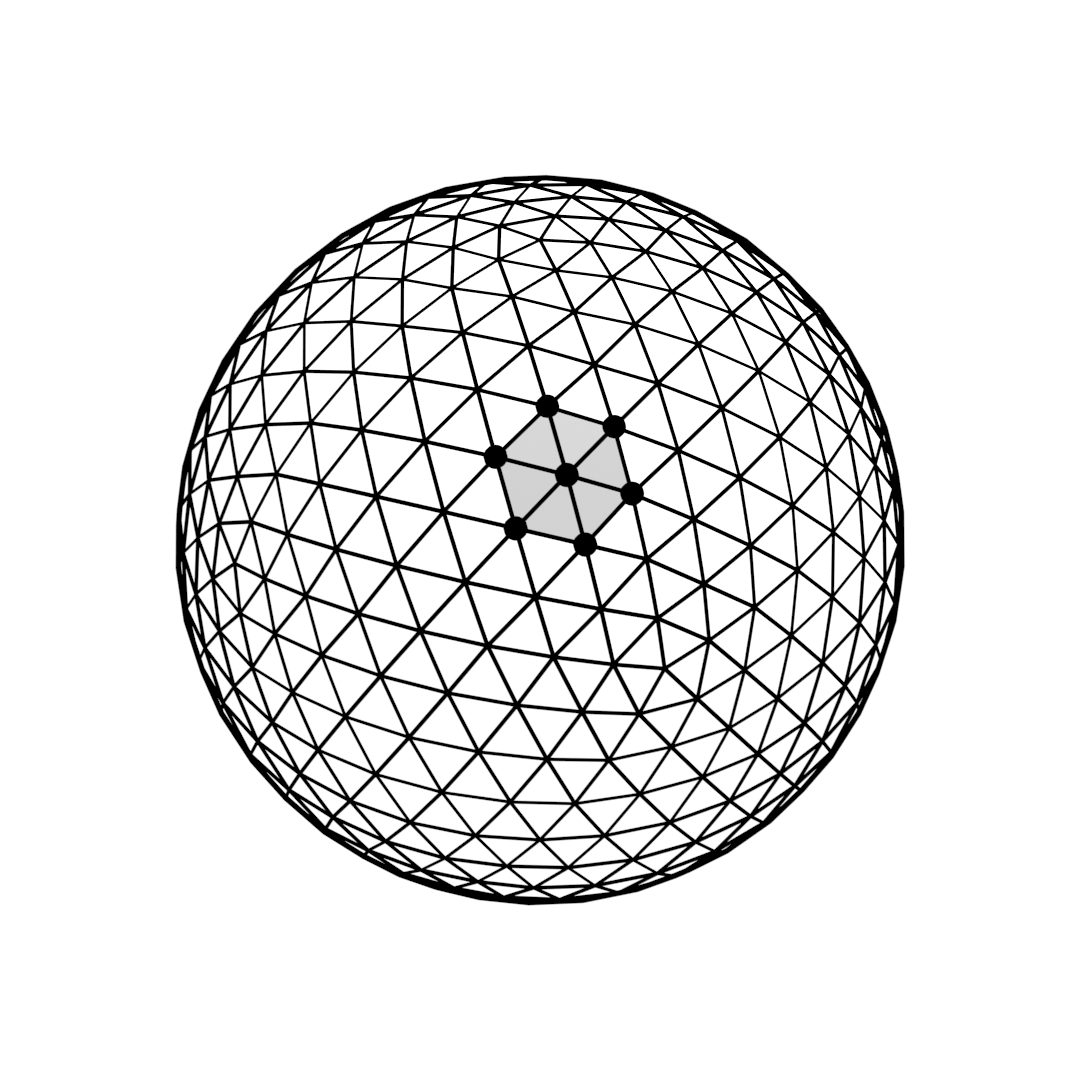
Meshes of a UV and an icosphere side-by-side. The neighbourhoods of a single vertex are highlighted.

An icosphere has this property. “Icosphere” is short for “icosahedral sphere” (at least that is what I think). This is because of how an icosphere is constructed: Starting with a regular icosahedron (which is just a fancy word for a three-dimensional shape whose faces are 20 equilateral triangles) we refine each of the faces by triangulating it and projecting the new vertices onto a sphere.

Construction of an icosphere. The icosahedron's faces are triangulated and then projected onto a sphre. Image from Wikipedia (CC BY-SA 4.0).

This results in a sphere where all the vertices are equally spaced, independent of the viewer’s position. Each vertex has six neighbours except for the original vertices of the icosahedron, which retain their count of five neighbours.

Original vertices of the icosahedron with only five neighbours.

In any case, an icosphere has much nicer properties than a UV sphere. The only disadvantage is that we now have a triangular grid where each vertex has five to six neighbours instead of four. This makes things a bit more complicated as we cannot just map the sphere’s surface to a rectangular grid anymore.

Simulation on an Iscosphere

On a rectangular grid, it is very easy to discretise the wave equation directly, resulting the five-point stencil mentioned above. We could also try to do this for a triangular grid but in order to keep things simple, I decided to ignore the wave equation for now and start with a simpler model:

Imagine for a moment that the water surface was made up of single “molecules” that are placed at each vertex of the mesh. Let’s also assume that each molecule is only affected by its direct neighbours (as it was the case on the rectangular grid as well). It now seems intuitive that each molecule’s neighbours “pull” on the molecule, exerting a force that is proportional to their displacement relative to the molecule (thus pulling the molecule upwards if they are higher and pulling it downwards if they are lower). We do not care about more complicated effects that would move the molecules parallel to the surface. We can this vertical displacement easily:

$\begin{aligned} \frac{\partial^2z}{\partial t^2} &= D \cdot \sum_{k \in K} \left( z_k - z \right) / \lvert K \rvert \\ &= D \cdot \left( \sum_{k \in K} z_k / \lvert K \rvert - z \right) \end{aligned}$

where $z$ is the displacement of the vertex (or molecule), $K$ is the (vertex) index set of the neighbouring vertices and $\lvert K \rvert$ is the number of neighbours. For the icosphere, $\lvert K \rvert$ is either 5 or 6. $D$ is an arbitrary constant. The attentive observer will have noticed that the formula above is actually just Hooke’s law $F = D \cdot \Delta l$ where $\Delta l$ equals the sum in the brackets. $D$ can then be interpreted as the spring constant. This means that the choice of $D$ will change the behaviour of the water surface.

Normally, we should also account for the distance between neighbouring vertices, but since the vertices are uniformly spaced on the icosphere this is not neccessary here.

There is still one more missing step to arriving at an equation that can be implemented in Godot and that is the discretisation of the time derivative on the left side of the formula (the upper index denotes current step in time):

$\begin{aligned} \frac{\partial^2z}{\partial t^2} \approx \frac{z^{t+1} - 2 \cdot z^t + z^{t-1}}{\Delta t^2} \end{aligned}$

Inserting this into the original formula, we arrive at

$\begin{aligned} \frac{z^{t+1} - 2 \cdot z^t + z^{t-1}}{\Delta t^2} &= D \cdot \sum_{k \in K} \left( z_k - z \right) / \lvert K \rvert\\ z^{t+1} &= a \cdot \sum_{k \in K} z_k^t / \lvert K \rvert + (2 - a) \cdot z^t - z^{t-1} \end{aligned}$

where we define $a = D \cdot \Delta t^2$. Since we will be using Godot’s physics process to update the simulation and Godot’s physics process uses a constant delta time, $\Delta t$ is just a constant which makes this possible.

The fact that this formula is almost identical to the rectangular grid should give us confidence.

To summarize: In order to retreive the updated displacement $z^{t+1}$, we need the current displacements $z_k^t$ of all neighbouring vertices, the number of neighbouring vertices $\lvert K \rvert$ as well as the current and previous displacements $z^t$ and $z^{t-1}$.

Implementation

A good way to implement the simulation would be to use compute shaders. We could pass this compute shader the neccessary information for each vertex (number and indices of neighbouring vertices as well as the displacement of each vertex) and then just apply the above formula to every vertex at every time step. Sadly, we are a bit limited, since Godot does not support compute shaders yet. Instead, we will again be using a fragment shader that renders to a separate viewport. We will pass all the neccessary information to the shader via textures. The color of the pixels in the viewport will then be the returned displacement values.

The setup in the editor is actually quite simple: The ColorRect has a material with the simulation shader assigned. By setting ColorRect as a child of SimulationViewport, the output of the shader is then rendered to SimulationViewport.

Vertices of a mesh can be numbered using vertex indices. Each vertex index of the icosphere corresponds to a pixel of the ColorRect: the displacement of the vertex with index $i$ would be rendered to the $i$th pixel of the ColorRect. We only count pixels along one axis, so all textures (input and render output) have dimension of (number of vertices x 1). The resulting textures can then be fed back to the shader after each simulation step to get $z^{t}$ and $z^{t-1}$.

Preprocessing in Blender

There are two problems left:

1. Each vertex of the icosphere needs the correct UVs (coordinates on the textures) assigned.
2. We need to pass the neighbours of each vertex to the shader.

I solved both of these problems by using a Blender script. The first problem is rather easy to solve: In Blender, all vertices of a mesh have an index available. We already stated that the vertex with index $i$ should correspond to the $i$th pixel on the displacement texture. Since UVs only go from 0 to 1, this means that the UV coordinate of each vertex should be $((\mathrm{vertex_index} + 0.5) / \mathrm{num_vertices}, 0)$ (we need to add 0.5 to make sure we hit the center of every pixel). In fact, given the index of a vertex (and the total number of vertices), we can retreive its UV coordinates at any time this way.

In Blender, assigning the UVs to the vertices of the icosphere looks somewhat like this:

for obj in bpy.context.selected_objects:
    num_verts = len(obj.data.vertices)

    bm = bmesh.new()
    bm.from_mesh(obj.data)
    uv_layer = bm.loops.layers.uv.active

    for face in bm.faces:
        for loop in face.loops:
            vert = loop.vert
            
            idx = vert.index
            uv = ((idx + 0.5) / num_verts, 0.0)
            loop[uv_layer].uv = uv

The second problem is a bit more complicated: We already know that each vertex has a maximum of six neighbours. We can thus use six textures to store this information. Let us call these textures n1 to n6. n1 will contain the vertex indices of the “first” neighbour of each vertex, n2 the the indices of the second and so forth. The way I organized this is illustrated below: Say, for example, the vertex with index 64 has the neighbours with the indices 63, 555, 554, 65, 564, and 561. As a result, the 64th pixel of n1 will contain the index 63, the same pixel of n2 will contain index 555 etc. In case a vertex has only five neighbours, we write a special value to the texture n6 to mark this.

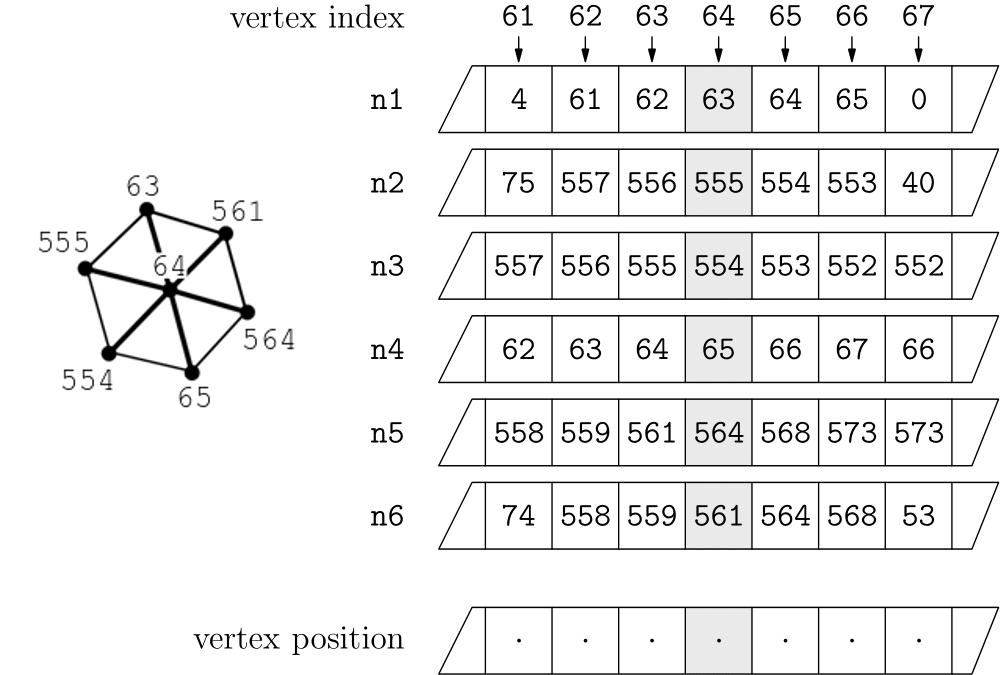
It will be important later on that consecutive neighbours share an edge (meaning that n1 and n2 should be connected as should n2 and n3 and so on). Additionally, I saved the vertex positions to a texture since we will also be needing them in the future.

The Simulation Shader

Now that we have created all neccessary textures containing the vertex neighbours, we can write a simulation shader that we assign to the ColorRect:

shader_type canvas_item;

uniform float a;

uniform sampler2D z_tex;
uniform sampler2D z_old_tex;

uniform sampler2D n1;
uniform sampler2D n2;
uniform sampler2D n3;
uniform sampler2D n4;
uniform sampler2D n5;
uniform sampler2D n6;

void fragment() {
    vec2 uv1 = getNeighbour(n1, UV);
    vec2 uv2 = getNeighbour(n2, UV);
    vec2 uv3 = getNeighbour(n3, UV);
    vec2 uv4 = getNeighbour(n4, UV);
    vec2 uv5 = getNeighbour(n5, UV);
    vec2 uv6 = getNeighbour(n6, UV);
    
    float num_n = 5.0f;
    vec2 sum_z = vec2(0.0f);
    sum_z += texture(z_tex, uv1).rg;
    sum_z += texture(z_tex, uv2).rg;
    sum_z += texture(z_tex, uv3).rg;
    sum_z += texture(z_tex, uv4).rg;
    sum_z += texture(z_tex, uv5).rg;

    if (uv6 != vec2(-1.0f)) {
        sum_z += texture(z_tex, uv6).rg;
        num_n++;
    }
    
    vec2 z = texture(z_tex, UV).rg;
    vec2 z_old = texture(z_old_tex, UV).rg;
    
    COLOR.rg = a * sum_z / num_n + (2.0f - a) * z - z_old;
}

z_tex and z_old_tex contain the current and the previous displacements. As before, n1 through n6 are one-dimensional textures which contain the indices of all the vertex neighbours. The function getNeighbour reads these indices from the corresponding textures and then calculates and returns the UVs or vec2(-1.0f) if the neighbour does not exist.

uniform float num_vertices = 642.0f;

vec2 getNeighbour(sampler2D n, vec2 uv) {
    vec4 c = texture(n, uv);
    if (c.a == 0.0f) {
        return vec2(-1.0f);
    }
    /* idx = (c.r * 255) << 8 + (c.g * 255) */
    float idx = c.r * 65280f + c.g * 255.0;
    return vec2((idx + 0.5) / num_vertices, 0.0f);
}

We then sum the displacements of all neighbours and calculate the new displacement using the formula from above. The new displacements are then rendered to the SimulationViewport. Notice that we are using both red and the green channel in our simulation. The red channel is used to store positive waves while the green channel stores negative waves. We can later just subtract the green channel from the red channel to retrieve the final displacement.

We also have to add a script to SimulationViewport that updates the simulation each physics frame by swapping textures and rendering a single frame to the Viewport:

func _update_map():
    var img = get_texture().get_data()
    simulation_material.get_shader_param("z_old_tex").set_data(simulation_material.get_shader_param("z_tex").get_data())
    simulation_material.get_shader_param("z_tex").set_data(img)

func _update():
    _update_map()
    render_target_update_mode = UPDATE_ONCE
    yield(get_tree(), "idle_frame")

func _physics_process(_delta):
    _update()

Displaying the Simulation on the Icosphere

We now have the simulation running but it is not displaying yet. In order to make that happen, we need to export the icosphere with the correct UVs from Blender and add it to the scene in Godot as a MeshInstance. Remember, each vertex UV corresponds to a pixel on the displacement texture from SimulationViewport.

We can thus write a simple shader that retrieves the displacement of each vertex and moves it outwards or inwards depending on the displacement value.

shader_type spatial;

uniform sampler2D vertex_position_tex;

void vertex() {
    VERTEX += normalize(VERTEX) * getDisplacement(UV);
    NORMAL = calculateVertexNormal(UV, VERTEX);
}

// Add fragment and lighting effects in the fragment() or light() functions.

A stated before, we subtract the green channel from the red channel to get the final displacement:

uniform sampler2D z_tex;

float getDisplacement(vec2 uv) {
    vec4 c = texture(z_tex, uv);
    return c.r - c.g;
}

And this is it! The sphere will now be deformed by the simulation.

CALCULATING VERTEX NORMALS

If order to achieve convincing lighting effects we also need to update the normals of each vertex.

For this, we need to know that the normal of a vertex is a weighted sum of the normals of all adjacent faces:

$\begin{aligned} \vec{N}_\mathrm{vert} = \sum w \cdot \vec{N}_\mathrm{face} \end{aligned}$

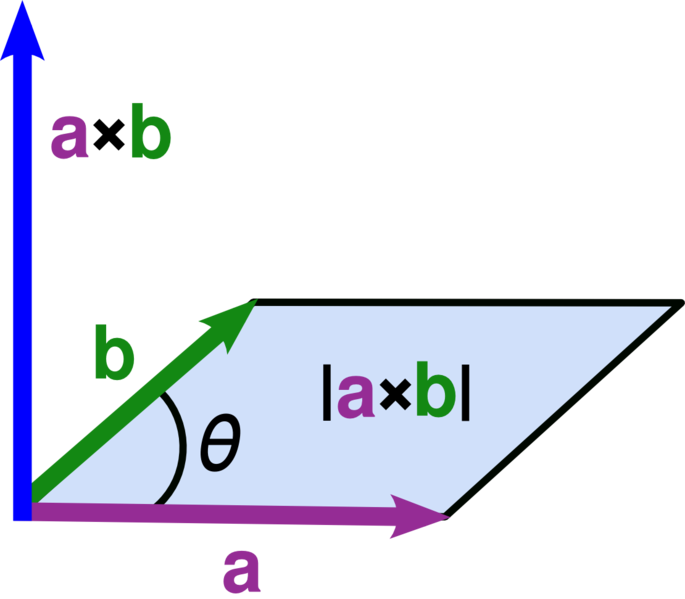
Calculating the face normals then is quite easy: The cross product, if you are not already familiar with it, of two vectors will produce a third vector that is perpendicular to both vectors and whose length is equal to the parallelogram they define.

Image from Wikipedia.

We can thus calculate a face normal that is weighted by the area of the face by taking the cross product of two edges of the face. Say $\vec{v}_0$, $\vec{v}_1$, and $\vec{v}_2$ are the three vertices of a face. We can then write:

$\begin{aligned} w \cdot \vec{N}_\mathrm{face} = \left( \vec{v}_1 - \vec{v}_0 \right) \times \left( \vec{v}_2 - \vec{v}_0 \right) \end{aligned}$

So to calculate a vertex normal we need the positions of all neighbouring vertices. We then calculate each weighted face normal using two connected neighbours, add all of them up and normalize the result.

The final shader code to calculate the vertex normals looks like this:

vec3 calculateVertexNormal(vec2 uv, vec3 v) {
    vec2 uv1 = getNeighbour(n1, uv);
    ...
    vec2 uv6 = getNeighbour(n6, uv);
    
    vec3 p1 = getPos(uv1);
    ...
    vec3 p5 = getPos(uv5);
    
    vec3 q1 = p1 + normalize(p1) * getDisplacement(uv1);
    ...
    vec3 q5 = p5 + normalize(p5) * getDisplacement(uv5);

    vec3 f1 = calculateFaceNormal(v, q1, q2);
    ...
    vec3 f4 = calculateFaceNormal(v, q4, q5);
    vec3 f5 = vec3(0.0f);
    vec3 f6 = vec3(0.0f);
    if (uv6 == vec2(-1.0f)) { // vertex has 5 neighbours
        f5 = calculateFaceNormal(v, q5, q1);
    } else { // vertex has 6 neighbours
        vec3 p6 = getPos(uv6);
        vec3 q6 = p6 + normalize(p6) * getDisplacement(uv6);
        f5 = calculateFaceNormal(v, q5, q6);
        f6 = calculateFaceNormal(v, q6, q1);	
    }
    
    vec3 n = vec3(0.0f);
    
    n += f1.xyz;
    ...
    n += f6.xyz;
    
    return normalize(n);
}

where getPos retreives the vertex position of the corresponding neighbour

uniform sampler2D vertex_position_tex;

vec3 getPos(vec2 uv) {
    return texture(vertex_position_tex, uv).xyz * 2.0f - 1.0f;
}

and calculateFaceNormal calculates the weighted normal of each face.

vec3 calculateFaceNormal(vec3 a, vec3 b, vec3 c) {
    vec3 n = cross(b - a, c - a);
    vec3 v = a + b + c;
    if (dot(v, n) < 0.0f) {
        n = -n;
    }
    return n;
}

We can now see why it was important to sort the neighbours earlier: If n2 was not a neighbour of n1, the resulting normal would not correspond to an actual face.

The correct normals an now be used inside the fragment() and light() processors to create convincing effects.

Player Interaction

You may have the feeling that we are missing one final part of the puzzle and by doing to you are quite correct. We have implemented the simulation as well as displaying it on a sphere. And while the ability to propagate waves across the sphere’s surface is nice, it is pretty useless without the ability to actually create waves. So I will briefly explain how interaction with the simulation could work:

I decided that the player should have the ability to create waves by clicking at any point on the sphere. Thus, detecting where on the sphere the mouse is, is the first step. In Godot, this can be easily done by adding a spherical CollisionShape to an Area. I can then use the Areas input_event to retrieve and store the position of the mouse click. I can then create waves directly in the fragment shader by manually setting displacement values based on the distance to the click position.

uniform vec4 click_position;

void fragment() {
    ...
	float click_dist = length(click_position.xyz - getPos(UV));
	if (click_dist < 0.15f) {
		if (click_position.a > 0.0f) {
			COLOR.r = (0.15f - click_dist) / 0.15f * click_position.w;
		} else {
			COLOR.g = (0.15f - click_dist) / 0.15f * -click_position.w;
		}
	}
}

By additionally setting the alpha value of the click_position uniform I can decide whether to create positive or negative waves. In order to conserve the volume of the sphere, it is a good idea to create first a positive wave and then shortly thereafter a negative wave for a single click, as only creating positive or negative waves would “bloat” or “shrink” the sphere.

Bonus: Boids

In order to fill the aquarium with some life, I decided to add schools of fish, often also called boids. My boid implementation is a pretty direct Godot translation of Sebastian Lague’s Unity implementation. If you want to know more about the theory behind boinds, check out his Coding Adventure video on the topic, it is a pretty interesting watch.

Thoughts and Conclusion

Although the scene turned out very nice, I still noticed some issues with the approach, mainly due to its relative simplicity. Besides some minor visual artifacts, the simulation is not very stable when trying to create slower moving waves. I could solve this by using an icosphere with more vertices but in that case the waves dissipate very quickyly. This is related to the simulation only taking into account direct neighbours and two previous timesteps. A more sophisticated method could (possibly at more computational cost) create a more stable, precise simulation.

I still hope you found this to be an interesting read. Please tell me on Twitter(@CaptainProton42) and Reddit (/u/CaptainProton42).